Déformation du disque solaire à l'horizon
![]()
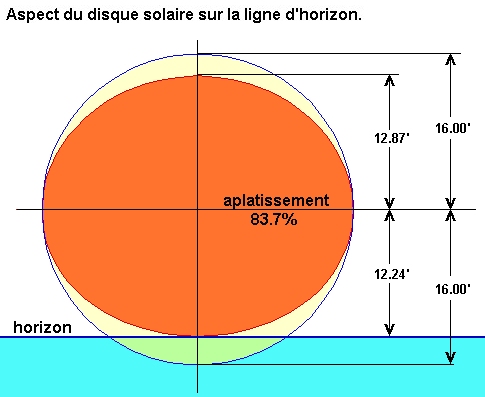
Aplatissement du disque solaire à l'horizon:
Bien que le phénomène d'aplatissement du soleil à l'horizon influence peu l'observation du Canigou, il m'a semblé intéressant d'aborder le sujet en tentant d'exploiter les formules de correction de la réfraction atmosphèrique.

La réfraction atmosphérique qui 'retarde' le coucher du soleil, et de la même façon 'accélère' son lever nous permet de profiter de quelques minutes supplémentaires d'ensoleillement chaque jour. Ses effets, comme le montre le dessin ci-dessus, sont particulièrement importants aux élévations angulaires inférieures à un degré; elle agit ainsi de façon différentielle entre le bord inférieur et supérieur de l'astre, introduisant un écrasement plus marqué dans la moitié inférieure. Ce phénomène, trés facilement observable sur un horizon bien dégagé, se produit aussi dans le cas de la lune.

Cette animation reprend la représentation du graphique ci-dessus. Cette simulation a été faite pour une pression de 1013 mb et à la température de 10°C. Le disque blanc correspond à la position réelle du soleil (dans le vide, sans air), tandis que le disque jaune est la position effectivement perçue par un observateur qui est à une altitude proche de l'horizon; si tel n'était pas le cas il faudrait alors tenir compte de la "dépression de l'horizon" pour l'altitude considérée.
L'animation permet aussi de mettre en évidence le retard de l'astre observé par rapport à sa position réelle dans son déplacement. Si on remonte le film à l'envers on obtient alors une avance qui correspond cette fois au lever de l'astre.
A noter aussi que l'animation montre une trajectoire verticale qui bien sûr ne correspond pas à la réalité, du moins à nos lattitudes. Le dessin précédent serait plus proche de la réalité, telle que nous pouvons l'appréhender dans nos régions, ce qui a pour conséquence de décaler l'azimut du coucher de l'astre!
 La
simulation, ici, prend comme hypothèse une pression atmoshérique
de 1013mb et une température au sol de 10°C.
La
simulation, ici, prend comme hypothèse une pression atmoshérique
de 1013mb et une température au sol de 10°C.
Quand le disque solaire touche la ligne de l'horizon, la position réelle de son centre est à 19 arcmin. en dessous de cette même ligne; ce qui, de centre à centre, donne un écart angulaire dù à la réfraction de presque 32 arcmin.
L'aplatisement se produit de façon différentielle entre le haut et le bas du disque; ce que l'on peut constater sur ce dessin par la différence calculée entre la moitié haute et la moitié basse du disque: entre 12,87 et 12,24 arcmin.
![]()
Aplatissement du disque lunaire à l'horizon:
Je remercie ici tout particulièrement le Dr James Behrens (Institute of Geophysics and Planetary Physics Scripps Institution of Oceanography ) pour son aimable autorisation à utiliser la photo de la lune qu'il a prise en Novembre 2005 et qui est parue sur le site de la NASA " la photo du jour" à la date du 25 Novembre. La photo a été prise à la station australienne Davis, en Antarctique.
REMARQUE IMPORTANTE: Il ne faut pas comparer directement les deux cas présentés sur cette page; celui du soleil exactement à l'horizon et celui de la lune à 10 arcmin au-dessus de l'horizon. Effectivement, l'effet différentiel de la réfraction agit de manière trés prononcée prés de l'horizon, et de plus les conditions climatiques sont différentes (pression et température). Ceci explique que l'applatisement du disque solaire soit beaucoup plus marqué que dans le cas de la lune.

Cette photo a sans doute été prise autour du 15 Novembre 2005 (pleine lune) vers 21h40 avec un diamètre apparent d'environ 32 arcmin. En utilisant la valeur du diamètre horizontal pratiquement pas altéré par la réfraction, soit 32 arcmin, on peut aisément en déduire la valeur du diamètre vertical qui est de 25.7 arcmin. L'applatissement peut alors être évalué à 80.4%.

En considérant que la Lune se trouve à environ 10 arcmin. au-dessus de l'horizon, et en utilisant les conditions locales de pression atmosphèrique de 980 mb et une température au sol de -2°C (hé oui, c'est ça l'été là-bas...), la simulation qui utilise la même formule que dans le cas du soleil donne un applatissement de 84.7% contre 80.4% sur la photo; soit un écart de moins de 6%, ce qui n'est pas si mal dans la mesure où cette simulation ne tient pas compte à la fois du degré hygrométrique de l'air et des conditions particuliéres d'un sol gelé.
 Le
dessin de gauche complète la simulation, il permet de constater
que la forme ovalisée n'est pas symétrique. En effet,
la partie supérieure mesure 13.89 arcmin., tandis que la
partie inférieure mesure 13.21 arcmin. Cette dissymétrie
représente envion 5%.
Le
dessin de gauche complète la simulation, il permet de constater
que la forme ovalisée n'est pas symétrique. En effet,
la partie supérieure mesure 13.89 arcmin., tandis que la
partie inférieure mesure 13.21 arcmin. Cette dissymétrie
représente envion 5%.
Voir le site Moonset from earth orbit qui présente une séquence d'images de la lune vue à travers différentes couches de l'atmosphère depuis la station spatiale internationale (ISS). L'effet d'aplatissement est des plus spectaculaires!
![]()
